Expectation Maximization and Variational Inference (Part 2)
In the previous post, we covered variational inference and how to derive update equations. In this post, we will go over a simple Gaussian Mixture Model with the Dirichlet prior distribution over the mixture weight.
Let $x_n$ be a datum and $z_n$ be the latent variable that indicates the assignment of the datum $x_n$ to a cluster $k$, $z_{nk} = I(z_n = k)$. We denote the weight of a cluster $k$ with $\pi_k$ and the natural parameter of the cluster as $\eta_k$.
The graphical model of the mixtures looks like the following.
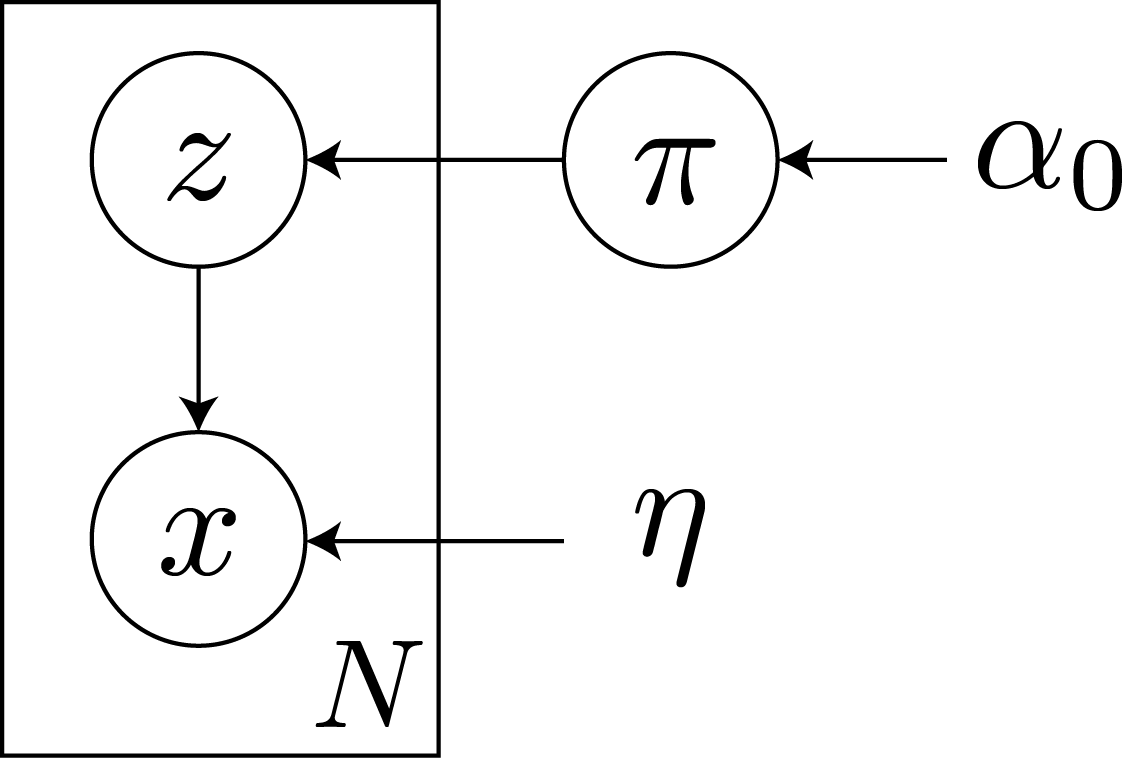
Formally, we define the generative process $p(\pi|\alpha), p(z_n; \pi_0), p(x_n | z_z, \eta)$. Unlike Bishop 1 and Blei et al. 2, we will not use prior over the natural parameter $\eta$ for simplicity. The notation and the model are similar to that used in Blei et al. 2. With overloading notation,
$$ \begin{align} p(\pi | \alpha_0) & = \mathrm{Dir}(\pi; \alpha_0) \\ p(z_n | \pi) & = \prod_k \pi_k^{z_{nk}} \\ p(x_n | z_n, \eta) & = \prod_k \mathcal{N}(x_n ; \eta_k)^{z_{nk}} \end{align} $$And the log joint probability is
$$ \log p(\mathbf{x}, \mathbf{z} ; \eta, \alpha_0) = \sum_n \sum_k z_{nk} [\log \pi_k + \log \mathcal{N}(x_n ; \eta_k)] + \log \mathrm{Dir}(\pi; \alpha_0) $$Meanfield Approximation
In this example, let’s use the meanfield approximation and make the posterior distribution of the latent variables $z$ and $\pi$ independent. i.e.
$$ q(z, \pi) = q(z)q(\pi) $$From the previous post, we know that the optimal distribution $q(\cdot)$ that maximizes the evidence lower bound is
$$ \log q(w_i) = \mathbb{E}_{w_{j}, j\neq i} \log p(x, \mathbf{w}) $$where $w_i$ is an arbitrary latent variable. Thus, we can use the same technique and find $q(z)$ and $q(\pi)$.
$$ \begin{align*} \log q(z) & = \sum_n \sum_k z_{nk} [\mathbb{E}\log \pi_k + \log \mathcal{N}(x_n ; \eta_k)] + \mathbb{E}\log \mathrm{Dir}(\pi; \alpha_0) \\ & = \sum_n \sum_k z_{nk} [\mathbb{E}\log \pi_k + \log \mathcal{N}(x_n ; \eta_k)] + C_1 \\ \log q(\pi) & = \sum_n \sum_k \mathbb{E}z_{nk} [\log \pi_k + \log \mathcal{N}(x_n ; \eta_k)] + \log \mathrm{Dir}(\pi; \alpha_0) \\ & = \sum_n \sum_k \mathbb{E}z_{nk} \log \pi_k + \log \mathrm{Dir}(\pi; \alpha_0) + C_2 \end{align*} $$We can easily compute the expectations of the latent variables.
$$ \begin{align*} \mathbb{E}\log \pi_k & = \psi(\alpha_k) - \psi(\sum_k \alpha_k) = \log \tilde{\pi}_k \\ \mathbb{E}z_{nk} & = q(z_{nk}=1) \propto \exp\left\{\log \tilde{\pi}_k + \log \mathcal{N}(x_n; \eta_k)\right\} = \rho_{nk} \\ \mathbb{E}z_{nk} & = \frac{\rho_{nk}}{\sum_l \rho_{nl}} = r_{nk} \end{align*} $$where $\alpha_k$ are the parameters of the latent variable $\pi_k$ and $\psi$ is the digamma function. We get the first equation from the property of the Dirichlet distribution. Given the expectations, we can simplify the equations and get update rules.
Expectation and Maximization
First, let’s examine the $\log q(\pi)$.
$$ \begin{align*} \log q(\pi) & = \sum_n \sum_k r_{nk} \log \pi_k + \log \mathrm{Dir}(\pi; \alpha_0) + C_2 \\ & = \sum_n \sum_k r_{nk} \log \pi_k + (\alpha_0 - 1) \log \pi_k + C_3 \\ & = \sum_k (\alpha_0 + \sum_n r_{nk} - 1) \log \pi_k + C_3 \\ & = \log \mathrm{Dir}(\pi| \alpha) \end{align*} $$Thus, $\alpha_k = \alpha_0 + \sum_n r_{nk}$. The $z$ update equation is given above. Finally, for $\eta$, we differentiate $p(x;\eta)$ with respect to $\eta$ to find the update rule.
$$ \begin{align*} \log p(x; \eta) & = \mathop{\mathbb{E}}_{z, \pi} \log p(x, z, \pi; \eta) \\ & = \sum_n \sum_k \mathbb{E} z_{nk} [\mathbb{E}\log \pi_k + \log \mathcal{N}(x_n ; \eta_k)] + \mathbb{E}\log \mathrm{Dir}(\pi; \alpha_0) \\ \nabla_{\eta_k} \log p(x; \eta) & = \sum_n r_{nk} \nabla_{\eta_k} \log \mathcal{N}(x_n ; \eta_k) \\ & = \sum_n r_{nk} \nabla_{\eta_k} \left( \frac{1}{2} \log |\Lambda_k| - \frac{1}{2} \mathrm{Tr}\left(\Lambda_k (x_n - \mu_n)(x_n - \mu_n)^T \right) \right) \\ \nabla_{\mu_k} \log p(x; \eta) & = \sum_n r_{nk} \Lambda_k (x_n - \mu_n) = 0 \\ \nabla_{\Lambda_k} \log p(x; \eta) & = \frac{1}{2} \sum_n r_{nk} \nabla_{\Lambda_k} \log |\Lambda_k| - r_{nk} \nabla_{\Lambda_k} \mathrm{Tr}\left(\Lambda_k (x_n - \mu_n)(x_n - \mu_n)^T \right) \\ & = \frac{1}{2} \sum_n r_{nk} \Lambda_k^{-1} - r_{nk} (x_n - \mu_n)(x_n - \mu_n)^T = 0 \\ \end{align*} $$From the above equations, we can get
$$ \begin{align} N_k & = \sum_n r_{nk} \\ \mu_k & = \frac{1}{N_k} \sum_n r_{nk} x_n \\ \Lambda_k & = \frac{1}{N_k} \sum_n r_{nk} (x_n - \mu_k)(x_n - \mu_k)^T \end{align} $$Evidence Lower Bound
Given the final solutions $r_{nk}$, $\log \tilde{\pi}_k$, $\alpha’$, we can derive the negative of the variational free energy, or the Evidence Lower Bound (ELBO).
$$ \begin{align*} ELBO & = \mathbb{E}_z \mathbb{E}_\pi \log \frac{p(x, z, \pi)}{q(z, \pi)} \\ & = \mathbb{E}_z \mathbb{E}_\pi \log \frac{p(x | z) p(z| \pi) p(\pi)}{q(z)q(\pi)} - \mathbb{E}_z\mathbb{E}_z \log q(z)q(\pi) \\ & = \underbrace{\mathbb{E}_z \log p(x | z)}_{\mbox{(a)}} + \underbrace{\mathbb{E}_z \mathbb{E}_\pi \log p(z | \pi) p(\pi) }_{\mbox{(b)}} + \underbrace{H(q(z))}_{\mbox{(c)}} + \underbrace{H(q(\pi))}_{\mbox{(d)}} \end{align*} $$where $H(\cdot)$ is the entropy. Each of the terms can be computed
$$ \begin{align*} \mbox{(a)} & = \mathbb{E}_z \log p(x | z) \\ & = \mathbb{E}_z \mathbb{E}_\pi \sum_n \sum_k z_{nk} \log \mathcal{N}_k(x_n) \\ & = \sum_n \sum_k r_{nk} \log \mathcal{N}_k(x_n) \\ \mbox{(b)} & = \mathbb{E}_z \mathbb{E}_\pi \log p(z | \pi) p(\pi) \\ & = \mathbb{E}_z \mathbb{E}_\pi \sum_n \log \frac{1}{B(\mathbb{\alpha}_0)} \prod_k \pi_k^{z_{nk}} \pi_k^{\alpha_0 - 1} \\ & = \mathbb{E}_z \mathbb{E}_\pi \sum_n \sum_k (z_{nk} + \alpha_0 - 1) \log \pi_k - \log B(\mathbb{\alpha}_0) \\ & = \sum_n \sum_k (\mathbb{E}_z z_{nk} + \alpha_0 - 1) \mathbb{E}_\pi \log \pi_k - \log B(\mathbb{\alpha}_0) \\ & = \sum_k \left( \sum_n r_{nk} + \alpha_0 - 1 \right) \log \tilde{\pi}_k - \log B(\mathbb{\alpha}_0) \\ \mbox{(c)} & = - \mathbb{E}_z \log q(z) \\ & = - \mathbb{E}_z \sum_n \sum_k z_{nk} \log r_{nk} \\ & = - \sum_n \sum_k r_{nk} \log r_{nk} \\ \mbox{(d)} & = - \mathbb{E}_\pi \log q(\pi) \\ & = - \mathbb{E}_\pi \log \frac{1}{B(\mathbb{\alpha}')} \prod_k \pi_k^{\alpha'_k - 1} \\ & = - \sum_k (\alpha'_k - 1) \log \mathbb{E}_\pi \pi_k + \log B(\mathbb{\alpha}') \\ & = - \sum_k (\alpha'_k - 1) \log \tilde{\pi}_k + \log B(\mathbb{\alpha}') \end{align*} $$Since $\log r_{nk} = \log \tilde{\pi}_k + \log \mathcal{N}_k(x_n) - \log \left( \sum_l \exp \{\log \tilde{\pi}_l + \log \mathcal{N}_l(x_n) \} \right)$,
$$ \begin{align*} \mbox{(a) + (c)} & = \sum_n \sum_k r_{nk} \left(\log \mathcal{N_k}(x_n) - \log r_{nk} \right) \\ & = \sum_n \sum_k r_{nk} \left(- \log \tilde{\pi}_k + \log \left( \sum_l \exp \{ \log \tilde{\pi}_l + \log \mathcal{N}_l(x_n) \} \right) \right)\\ & = - \sum_k N_k \log \tilde{\pi}_k + \sum_n \log \left( \sum_l \exp \{ \log \tilde{\pi}_l + \log \mathcal{N}_l(x_n) \} \right) \\ \mbox{(b) + (d)} & = \sum_k \left( \sum_n r_{nk} + \alpha_0 - 1 \right) \log \tilde{\pi}_k - \log B(\mathbb{\alpha}_0) \\ & - \sum_k (\alpha'_k - 1) \log \tilde{\pi}_k + \log B(\mathbb{\alpha}') \\ & = \sum_k \left( \sum_n r_{nk} + \alpha_0 - \alpha'_k \right) \log \tilde{\pi}_k - \log B(\mathbb{\alpha}_0) + \log B(\mathbb{\alpha}') \\ & = \log B(\mathbb{\alpha}') - \log B(\mathbb{\alpha}_0) \end{align*} $$Thus,
$$ \begin{align*} ELBO = & \mathbb{E}_z \mathbb{E}_\pi \log \frac{p(x, z, \pi)}{q(z, \pi)} \\ = & - \sum_k N_k \log \tilde{\pi}_k + \sum_n \log \left( \sum_l \exp \{ \log \tilde{\pi}_l + \log \mathcal{N}_l(x_n) \} \right) \\ & + \log B(\mathbb{\alpha}') - \log B(\mathbb{\alpha}_0) \\ \end{align*} $$References
C. Bishop, Pattern Recognition and Machine Learning. Springer, 2006 ↩
Blei, Variational Inference for Dirichlet Process Mixtures, Bayesian Analysis 2006 ↩ ↩2


Leave a Comment